路遥的小书屋

深色模式

OpenGL 知识 ​

浏览器上的WebGL，和Android中的OpenGL ES，原理相同，API命名也基本一致。

参考资料 ​

  1. OpenGL入门教程：大名鼎鼎的LearnOpenGL CN。

  2. 文档：GLSL 2.0语法。

  3. 文档：OpenGL ES api文档

  4. WebGL入门教程：这里有源码和教程目录，我fork了这个项目：

    https://github.com/yuluyao/WebGLTutorial。

  5. Android OpenGL ES入门：

    https://blog.csdn.net/gongxiaoou/article/details/89199632

  6. Android OpenGL ES NDK入门，写得有点乱，暂时没有找到更好的。

    https://www.zybuluo.com/cxm-2016/note/544209

OpenGL概念 ​

低级图形库与高级图形库 ​

高级图形库 ​

  1. Skia：用于Android、Flutter、Google Chrome
  2. CoreAnimation：用于iOS

低级图形库 ​

  1. OpenGL：跨平台，应用最广
  2. Vulkan：跨平台，比较新，未普及
  3. Metal：只用于Apple家
  4. DrectX3D：Windows

OpenGL、WebGL、OpenGL ES的关系 ​

简单地说： ​

  1. OpenGL是跨平台的。
  2. OpenGL ES是OpenGL在移动设备上的实现，它是OpenGL的子集。
  3. WebGL是OpenGL在Web端的实现，与OpenGL ES类似，它是OpenGL的子集。

图解： ​

用图片来解释三者的关系：

img

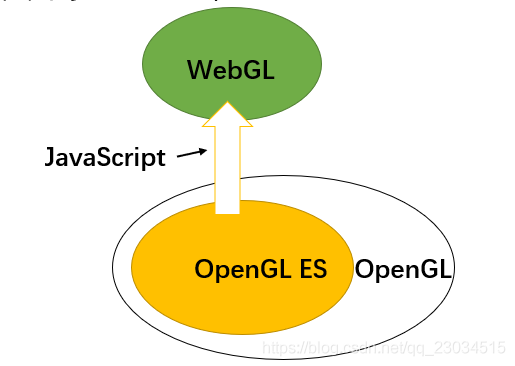
具体版本的对应关系：

img

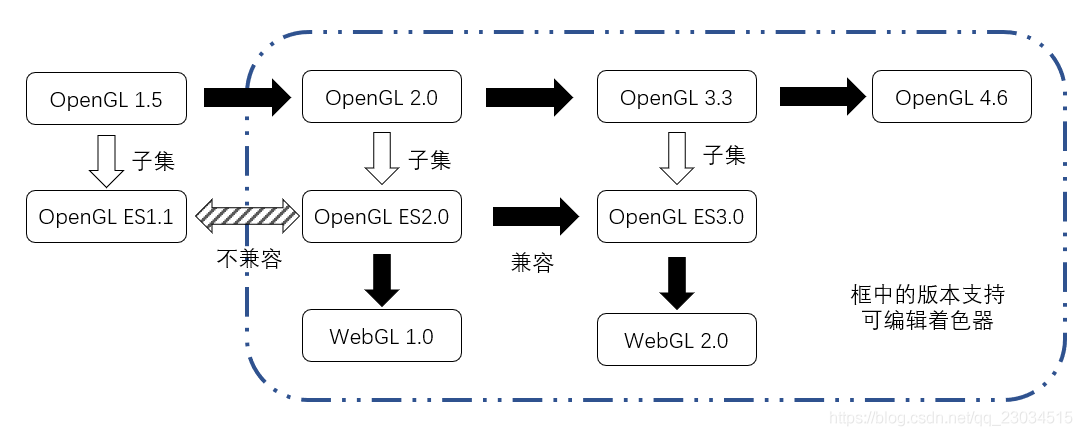
图形学：理解齐次坐标 ​

参考： ​

https://blog.csdn.net/janestar/article/details/44244849

我的理解： ​

齐次坐标(1, 2, 3)、(2, 4, 6)、(4, 8, 12)代表二维笛卡尔坐标系中的同一个点：(1/3, 2/3)，我们说这3个坐标是齐次的。

同样的原理，可以推广的3维坐标系中。

图形学：图形变换矩阵 ​

模型变换 ​

  1. 旋转变换

    $$ R_{z}=\left[\begin{array}{cccc}\cos \beta & -\sin \beta & 0 & 0 \ \sin \beta & \cos \beta & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1\end{array}\right] $$

    $$ R_{x}=\left[\begin{array}{cccc}1 & 0 & 0 & 0 \ 0 & \cos \beta & -\sin \beta & 0 \ 0 & \sin \beta & \cos \beta & 0 \ 0 & 0 & 0 & 1\end{array}\right] $$

    $$ R_{y}=\left[\begin{array}{cccc}\cos \beta & 0 & \sin \beta & 0 \ 0 & 1 & 0 & 0 \ -\sin \beta & 0 & \cos \beta & 0 \ 0 & 0 & 0 & 1\end{array}\right] $$

  2. 平移变换

    $$ T=\left[\begin{array}{cccc}1 & 0 & 0 & T x \ 0 & 1 & 0 & T y \ 0 & 0 & 1 & T z \ 0 & 0 & 0 & 1\end{array}\right] $$

  3. 缩放变换

    $$ S=\left[\begin{array}{cccc}S x & 0 & 0 & 0 \ 0 & S y & 0 & 0 \ 0 & 0 & S z & 0 \ 0 & 0 & 0 & 1\end{array}\right] $$

视图变换 ​

$$ V=R^{-1} T^{-1}=\left[\begin{array}{cccc}U x & U y & U z & 0 \ V x & V y & V z & 0 \ N x & N y & N z & 0 \ 0 & 0 & 0 & 1\end{array}\right] *\left[\begin{array}{cccc}1 & 0 & 0 & -T x \ 0 & 1 & 0 & -T y \ 0 & 0 & 1 & -T z \ 0 & 0 & 0 & 1\end{array}\right]=\left[\begin{array}{cccc}U x & U y & U z & -U \cdot T \ V x & V y & V z & -V \cdot T \ N x & N y & N z & -N \cdot T \ 0 & 0 & 0 & 1\end{array}\right] $$

投影变换 ​

  1. 透视投影

    $$ P=\left[\begin{array}{cccc}\frac{1}{\text { aspect*tan }\left(\frac{\text { fovy }}{2}\right)} & 0 & 0 & 0 \ 0 & \frac{1}{\tan \left(\frac{\text { fovy }}{2}\right)} & 0 & 0 \ 0 & 0 & \frac{f+n}{n-f} & \frac{2 f n}{n-f} \ 0 & 0 & -1 & 0\end{array}\right] $$

  2. 正射投影

    $$ O=\left[\begin{array}{cccc}\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \ 0 & 0 & -\frac{2}{f-n} & -\frac{f+n}{f-n} \ 0 & 0 & 0 & 1\end{array}\right] $$

GLSL 2.0中的变量限定符： ​

  1. attribute

    attribute 变量只用于顶点着色器中，用来存储顶点着色器中每个顶点的输入（per-vertex inputs）。attribute 通常用来存储位置坐标、法向量、纹理坐标和颜色等。注意 attribute 是用来存储单个顶点的信息。

  2. uniform

    用于存储应用程序通过 GLSL 传递给着色器的只读值。uniform 可以用来存储着色器需要的各种数据，如变换矩阵、光参数和颜色等。传递给着色器的在所有的顶点着色器和片段着色器中保持不变的的任何参数，基本上都应该通过 uniform 来存储。

    需要注意的一点是，顶点着色器和片段着色器共享了 uniform 变量的命名空间。对于连接于同一个着色程序对象的顶点和片段着色器，它们共用同一组 uniform 变量，因此，如果在顶点着色器和片段着色器中都声明了 uniform 变量，二者的声明必须一致。当应用程序通过 API 加载了 uniform 变量时，该变量的值在顶点和片段着色器中都能够获取到。

  3. varying

    varying 存储的是顶点着色器的输出，同时作为片段着色器的输入，通常顶点着色器都会把需要传递给片段着色器的数据存储在一个或多个 varying 变量中。这些变量在片段着色器中需要有相对应的声明且数据类型一致，然后在光栅化过程中进行插值计算。

  4. const

  5. 默认